I. Les Ensembles (Sets)
Les ensembles sont l’une des bases fondamentales des mathématiques et constituent une notion clé pour décrire des collections d’objets. Un ensemble est simplement un groupe d’éléments distincts (indépendants), qui peuvent être des nombres, des points, des polynômes, des vecteurs, ou même des concepts abstraits. Cette flexibilité est importante, car elle nous permet de manipuler et de structurer des éléments divers pour mieux comprendre des phénomènes ou résoudre des problèmes.
En mécanique et en robotique, les ensembles permettent de regrouper des informations utiles, comme un ensemble de points dans l’espace ou des ensembles de paramètres spécifiques. Ils permettent également de d’identifier la nature des objets mathématiques que nous manipulons.
On peut définir un ensemble de deux façon. Soit en listant les éléments qu’il contient, soit en décrivant les hypothèses ou propriétés que respectent les éléments qu’il contient.
Exemple :
On peut aussi écrire cette ensemble de cette façon :
A la fin de ce chapitre vous serez capable de lire et même de définir vos propres ensembles !
In english please !
Set: a collection of distinct objects or elements.
1. Notation et Symboles des Ensembles
Les ensembles sont généralement notés avec des lettres majuscules, comme \( A \), \( B \), ou \( S \). Les éléments d’un ensemble sont placés entre accolades { }, et on les sépare par des virgules. Par exemple, si l’on veut décrire l’ensemble des trois premiers nombres naturels, on peut écrire :
Dans ce cas, 1, 2, et 3 sont des éléments de l’ensemble A.
Si un élément appartient à un ensemble, on utilise le symbole ∈. Par exemple, pour exprimer que 1 est dans A, on écrit :
In english please !
Element: an individual object within a set, often represented with the symbol ∈ to indicate “belongs to.”
2. Types d’Ensembles
Il existe différents types d’ensembles ainsi qu’un vocabulaire particulier pour les décrire.
On parle par exemple de :
- Ensemble vide \( \emptyset \) : Un ensemble qui ne contient aucun élément. Par exemple, l’ensemble des solutions d’une équation sans solution.
- Ensemble fini : Un ensemble avec un nombre limité d’éléments, comme \( B = \{a, b, c\} \).
- Ensemble infini : Un ensemble avec un nombre illimité d’éléments, comme l’ensemble des nombres naturels \( N = \{1, 2, 3, \dots\} \).
Les ensembles peuvent regrouper différents types d’objets, par exemples :
- Des nombres (comme les entiers ou réels),
- Des points,
- Des polynômes,
- Des vecteurs,
- Ou même des matrices.
Cette possibilité de rassembler divers objets mathématiques dans des ensembles prépare les bases pour des structures mathématiques plus complexes comme les espaces vectoriels.
In english please !
- Empty set: a set with no elements, often represented by ∅ or {}.
- Finite set: a set with a finite number of elements.
- Infinite set: a set with an infinite number of elements.
3. Opérations sur les Ensembles
Il est possible de réaliser différentes opérations sur les ensembles qui nous seront utiles dans des situations pratiques, en particulier pour organiser et manipuler les données. Voici quelques unes des opérations les plus communes :
- Union \( A \cup B \) : L’union de deux ensembles \( A \) et \( B \) est l’ensemble de tous les éléments présents dans A ou dans B (ou dans les deux). Par exemple, si \( A = \{1, 2\} \) et \( B = \{2, 3\} \), alors :
- Intersection \( A \cap B \) : L’intersection de deux ensembles \( A \) et \( B \) est l’ensemble de tous les éléments présents à la fois dans A et dans B. Par exemple, avec \( A = \{1, 2\} \) et \( B = \{2, 3\} \), on obtient :
- Différence \( A \setminus B \) : La différence entre deux ensembles A et B est l’ensemble des éléments qui sont dans A mais pas dans B. On peut aussi lire cela “A moins les éléments contenus dans B”. Par exemple, avec \( A = \{1, 2\} \) et \( B = \{2, 3\} \), on a :
In english please !
- Union: the set of all elements in either or both sets, represented as A \cup B.
- Intersection: the set of all elements in existing in both sets, represented as A \cap B.
Exercice
Essayez de répondre aux questions suivantes pour pratiquer l’utilisation des ensembles :
- Soit \( C = \{4, 5, 6\} \) et \( D = \{5, 6, 7\} \). Quelle est l’union de \( C \) et \( D \) ?
- Quelle est l’intersection de \( C \) et \( D \) ?
- Quelle est la différence entre \( C \) et \( D \) (c’est-à-dire, \( C \setminus D \)) ?
- \(C \cup D = \{4, 5, 6, 7\}\)
- \(C \cap D = \{5, 6\}\)
- \(C \setminus D = \{4\}\)
4. Définir un Ensemble par une Règle
Il est possible de définir un ensemble non seulement en énumérant ses éléments, mais aussi en utilisant une règle qui décrit ses propriétés. Par exemple, si l’on souhaite définir un ensemble contenant les trois premiers mois de l’année, on peut écrire :
Dans ce cas, l’ensemble A sera équivalent à :
In english please !
Set described by rule: a set definition based on a specific rule or property of its elements, such as \( A = \{ x | \ x \ \text{has a specific property}\} \).
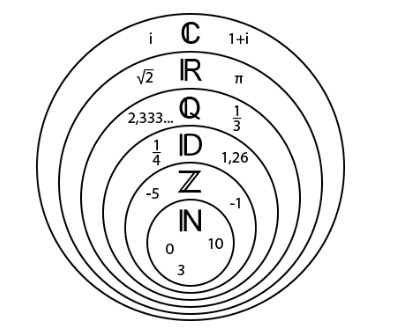
5. Les Ensembles Fixes
Certains ensembles sont fréquemment utilisés dans les mathématiques et possèdent des notations standard que vous rencontrerez souvent :
- \( \mathbb{N} \) : Ensemble des nombres naturels \( \mathbb{N} = \{0, 1, 2, 3, \dots\} \)
- \( \mathbb{Z} \) : Ensemble des nombres entiers \( \mathbb{Z} = \{\dots, -2, -1, 0, 1, 2, \dots\} \)
- \( \mathbb{Q} \) : Ensemble des nombres rationnels (nombres pouvant être exprimés comme le rapport de deux entiers) \( \mathbb{Q} = \left\{\frac{a}{b} \ | \ a \in \mathbb{Z}, b \in \mathbb{Z}^*, b \neq 0 \right\} \)
- \( \mathbb{R} \) : Ensemble des nombres réels (incluant tous les nombres rationnels et irrationnels comme √2, π).
Les tips de top-top
Dans certains cas la présence de l’élément 0 dans un ensemble peut être ambigüe. Pour éviter les confusions il convient de préciser si l’on choisi d’inclure 0 ou pas. Pour les entiers naturels par exemple on écrira \(N_0\) ou \({N}^*\cup \{0\}\) pour signifier que l’on inclus l’élément neutre. Au contraire on écrira \({N}^*\) ou \({N}\setminus0\) pour préciser que l’on exclus 0
In english please !
Fixed sets: standard sets commonly used in mathematics, such as the natural numbers \( \mathbb{N} \), integers \( \mathbb{Z} \), rational numbers \( \mathbb{Q} \), and real numbers \( \mathbb{R} \).
6. Notation des Intervalles
Pour définir des sous-ensembles de nombres réels, nous utilisons souvent la notation d’intervalles, qui permet de préciser si les limites d’un ensemble sont incluses ou non. Voici les principales conventions :
- Intervalle ouvert \( (0, 1) \) : Contient tous les nombres entre 0 et 1, sans inclure 0 ni 1.
- Intervalle fermé \( [0, 1] \) : Contient tous les nombres entre 0 et 1, y compris 0 et 1.
- Intervalle semi-ouvert \( (0, 1] \) : Contient tous les nombres entre 0 et 1, incluant 1 mais excluant 0.
Ces notations permettent de préciser les limites de l’ensemble et sont très utiles pour décrire des plages de valeurs, notamment en physique ou en ingénierie.
In english please !
Intervals: notation to define subsets of real numbers, specifying whether boundaries are included (e.g., \( (a, b) \), \( [a, b] \)).
8. Stabilité et propriétés de ℝ
L’ensemble des nombres réels \( \mathbb{R} \) possède plusieurs propriétés fondamentales qu’il est important de connaître. Mais l’ensemble des nombre réel est surtout un bon moyen pour le professeur d’introduire la notion de stabilité (ou clôture).
8.1 Définition de la Stabilité
Un ensemble est dit stable (ou clos) pour une opération définie, si, pour tous les éléments de cet ensemble, le résultat de l’opération appartient encore au même ensemble. Cela signifie que lorsqu’on applique une opération comme l’addition, la multiplication ou la soustraction sur des éléments de l’ensemble, le résultat doit rester dans l’ensemble, sinon on dit que l’ensemble n’est pas clos pour l’opération.
En d’autres termes, un ensemble \( E \) est stable sous une opération \( \star \) si, pour tous \( a \) et \( b \) dans \( E \), \( a \star b \in E \).
On peut également démontrer d’une partie finie de l’ensemble est stable pour une opération bien que l’ensemble de départ ne l’est pas nécessairement.
8.2 Propriétés de ℝ
L’ensemble des nombres réels \( \mathbb{R} \) possède plusieurs propriétés fondamentales. Voici quelques-unes de ces propriétés les plus importantes :
-
Fermeture pour l’addition : La somme de deux nombres réels est toujours un nombre réel. Par exemple, \( 2 + 5 = 7 \), et \( 7 \in \mathbb{R} \).
-
Fermeture pour la multiplication : Le produit de deux nombres réels est également un nombre réel. Par exemple, \( 3 \times 4 = 12 \), et \( 12 \in \mathbb{R} \).
-
Élément neutre pour l’addition : L’élément \( 0 \) agit comme un neutre pour l’addition. Cela signifie que, pour tout \( x \in \mathbb{R} \), \( x + 0 = x \). Par exemple, \( 5 + 0 = 5 \).
-
Inverse pour l’addition : Chaque nombre réel possède un inverse pour l’addition, ce qui signifie qu’il existe un nombre réel \( -x \) tel que \( x + (-x) = 0 \). Par exemple, pour \( 3 \), l’inverse est \( -3 \) car \( 3 + (-3) = 0 \).
-
Distributivité : La multiplication est distributive par rapport à l’addition, ce qui signifie que \( x \times (y + z) = x \times y + x \times z \) pour tout \( x, y, z \in \mathbb{R} \). Par exemple, \( 2 \times (3 + 4) = 2 \times 3 + 2 \times 4 = 14 \).
Ces propriétés garantissent que les nombres réels forment une structure cohérente et robuste pour les opérations mathématiques.
8.3 Exemple : Stabilité des Nombres Naturels Positifs
Considérons l’ensemble des nombres naturels positifs \( \mathbb{N}^+ = \{1, 2, 3, \dots\} \).
-
Stabilité sous l’addition : La somme de deux nombres naturels positifs est toujours un nombre naturel positif. Par exemple, si \( 2 \in \mathbb{N}^+ \) et \( 3 \in \mathbb{N}^+ \), alors \( 2 + 3 = 5 \in \mathbb{N}^+ \). On dit donc que \( \mathbb{N}^+ \) est stable sous l’addition.
-
Non-stabilité sous la soustraction : La soustraction de deux nombres naturels positifs peut donner un résultat qui n’est pas un nombre naturel positif. Par exemple, \( 3 - 5 = -2 \), qui n’appartient pas à \( \mathbb{N}^+ \). Ainsi, \( \mathbb{N}^+ \) n’est pas stable sous la soustraction.
La compréhension de la stabilité est essentielle, car elle indique les limites de l’ensemble et si d’autres méthodes ou ensembles peuvent être nécessaires pour certaines opérations.
Exercice
Déterminez si les ensembles suivants sont stables sous les opérations indiquées :
- Les nombres pairs sous l’addition : Si \( a \) et \( b \) sont des nombres pairs, est-ce que \( a + b \) est également pair ?
- Les nombres entiers \( \mathbb{Z} \) sous la division : Si \( a \) et \( b \) sont des entiers, est-ce que \( a \div b \) est toujours un entier ?
- Les multiples de 3 sous la soustraction : Si \( a \) et \( b \) sont multiples de 3, est-ce que \( a - b \) est toujours un multiple de 3 ?
- Oui, les nombres pairs sont stables sous l’addition car la somme de deux nombres pairs est toujours paire.
- Non, \( \mathbb{Z} \) n’est pas stable sous la division car la division de deux entiers peut produire un nombre rationnel. Par exemple, \( 4 \div 3 = 1.33 \), qui n’est pas un entier.
- Oui, les multiples de 3 sont stables sous la soustraction, car la différence de deux multiples de 3 est toujours un multiple de 3.
9. Utilisation des Symboles pour Définir des Ensembles
Pour définir des ensembles de façon concise, on utilise souvent une notation mathématique plus formelle. Cette notation permet d’exprimer les ensembles et leurs propriétés sans avoir à énoncer chaque élément individuellement.
9.1 Principaux Symboles et Leur Signification
| Symbole | Signification | Description |
|---|---|---|
| \( \in \) | Appartenance | Un élément appartient à un ensemble, ex. \( x \in A \) signifie que \( x \) est un élément de \( A \). |
| \( \subset \) | Sous-ensemble | Indique que tous les éléments d’un ensemble \( A \) sont aussi dans un ensemble \( B \), \( A \subset B \). |
| \( \cup \) | Union | Réunion de deux ensembles, contenant tous les éléments de \( A \) et de \( B \). |
| \( \cap \) | Intersection | Ensemble des éléments communs à \( A \) et \( B \). |
| \( \forall \) | Pour tout | Indique que quelque chose est vrai pour chaque élément d’un ensemble, ex. \( \forall x \in \mathbb{R} \). |
| \( \exists \) | Il existe | Indique qu’au moins un élément satisfait une condition, ex. \( \exists x \in A \). |
| \( \exists ! \) | Il existe un unique | Indique qu’il existe un seul élément vérifiant la condition, ex. \( \exists ! x \in A \) tel que … |
A ces notations s’ajoutent toutes les notations communes tels que les opérateurs de comparaisons et autres (\(>\), \(<\), \(\leq\) …)
9.2 Exemples de Définition d’Ensembles avec Notation
- L’ensemble des nombres pairs positifs peut être défini par une notation concise :
- L’ensemble des nombres réels positifs peut être défini par :
Exercice
Créez des ensembles en utilisant la notation mathématique formelle pour exprimer les propriétés suivantes :
- L’ensemble des multiples de 3 dans les entiers naturels \( \mathbb{N} \).
- L’ensemble des nombres négatifs dans \( \mathbb{Z} \).
- L’ensemble des carrés parfaits dans \( \mathbb{N} \) (nombres pouvant s’écrire comme \( n^2 \), où \( n \in \mathbb{N} \)).
- \( M = \{ x \in \mathbb{N} \ | \ x = 3k, \ k \in \mathbb{N} \} \)
- \( N = \{ x \in \mathbb{Z} \ | \ x < 0 \} \)
- \( S = \{ x \in \mathbb{N} \ | \ x = n^2, \ n \in \mathbb{N} \} \)
10. Corps
Un corps (en anglais, field) est un ensemble \( \mathbb{K} \) muni de deux opérations, l’addition \( + \) et la multiplication \( \times \), satisfaisant les propriétés suivantes :
\( (\mathbb{K}, +) \) est un groupe commutatif :
- Associativité de l’addition : \( \forall a, b, c \in \mathbb{K}, \ (a + b) + c = a + (b + c) \).
- **Élément neutre de l’addition : Il existe un élément \( 0 \in \mathbb{K} \) tel que \( \forall a \in \mathbb{K}, \ a + 0 = a \).
- Inverse additif** : \( \forall a \in \mathbb{K}, \ \exists (-a) \in \mathbb{K} \) tel que \( a + (-a) = 0 \).
- Commutativité de l’addition : \( \forall a, b \in \mathbb{K}, \ a + b = b + a \).
\( (\mathbb{K} \setminus \{0\}, \times) \) est un groupe commutatif :
- Associativité de la multiplication : \( \forall a, b, c \in \mathbb{K} \setminus \{0\}, \ (a \times b) \times c = a \times (b \times c) \).
- Élément neutre de la multiplication : Il existe un élément \( 1 \in \mathbb{K}, \ 1 \neq 0 \) tel que \( \forall a \in \mathbb{K}, \ a \times 1 = a \).
- Inverse multiplicatif : \( \forall a \in \mathbb{K} \setminus \{0\}, \ \exists a^{-1} \in \mathbb{K} \) tel que \( a \times a^{-1} = 1 \).
- Commutativité de la multiplication : \( \forall a, b \in \mathbb{K}, \ a \times b = b \times a \).
- Distributivité de la multiplication par rapport à l’addition :
- \( \forall a, b, c \in \mathbb{K}, \ a \times (b + c) = (a \times b) + (a \times c) \).
Les exemples courants de corps sont :
- Les nombres rationnels \( \mathbb{Q} \)
- Les nombres réels \( \mathbb{R} \)
- Les nombres complexes \( \mathbb{C} \)
11. Bonus - Implication et Équivalence
En mathématiques, il est souvent utile de pouvoir relier des affirmations ou expressions pour montrer comment elles dépendent les unes des autres. Ces relations sont décrites par les notions d’implication et d’équivalence.
Implication : Si une affirmation 1 (S1) entraîne nécessairement une affirmation 2 (S2), on dit que S1 implique S2. On note cela
Ce symbole signifie que si S1 est vraie, alors S2 doit également être vraie. Cependant, cela ne signifie pas nécessairement que S2 implique S1.
In english please !
Statement 1 implies Statement 2: when S1 is true, S2 must also be true.
Équivalence : Si deux affirmations S1 et S2 sont vraies l’une en fonction de l’autre, on dit qu’elles sont équivalentes et qu’elles s’impliquent mutuellement. Cela signifie que si S1 est vraie, alors S2 est également vraie, et inversement. On note cela :
Cette notation signifie que les deux affirmations sont logiquement équivalentes.
In english please !
S1 if and only if S2: they are equivalent since they imply each other.
Exemple
Prenons un exemple simple pour illustrer ces concepts :
Implication : Si un nombre \( x \) est divisible par 4, alors il est également divisible par 2. On peut écrire :
Cette implication est vraie, car tout nombre divisible par 4 est également divisible par 2, mais l’inverse n’est pas forcément vrai (par exemple, 6 est divisible par 2, mais pas par 4).
Équivalence : Si \( x \) est un nombre pair, alors \( x \) est divisible par 2. Cela est aussi vrai dans l’autre sens : si \( x \) est divisible par 2, alors \( x \) est un nombre pair. On peut donc écrire :
Cette équivalence montre que les deux affirmations sont vraies l’une par rapport à l’autre. Ces concepts d’implication et d’équivalence permettent de structurer les raisonnements mathématiques et de démontrer des liens logiques entre différentes propositions.